Note: Cornell Pump Market Managers provide periodic articles to the blog, to discuss issues and developments and pump. The articles are meant to be more conversation and less technical, while still explaining important pumping concepts. In this edition, Cornell Pump Industrial Market Manager Derek Petersen discusses a method to determine suction lift.
People always ask how much of a suction lift will a Cornell Pump pull? The answer is simple and easy to calculate in four steps:
- Determine the NPSHR (provided on pump curve)
- Look up the amount of pressure the atmosphere (weight of air) is pushing down at a particular elevation.
- Calculate how much energy all the valves, pipe, fittings, elbows, etc., in the pump system cost the system in terms of flow.
- Compare how much the system could produce versus how much energy it going to cost.
The first thing to understand is that every pump has an energy requirement needed to run without cavitation. This required energy is call the Net Positive Suction Head Required or NPSHR. Thinking of NPSHR another way, it’s the absolute pressure a liquid must have to avoid creating microscopic, damaging vapor bubbles in the liquid being pumped. Those bubbles are cavitation and they can harm a pump and shorten its useable life.
The NPSHR is inherently part of the pump design [how steep the impeller vanes, the speed of operation, the shape of the volute, etc.,] and is listed on the pump curve at your specific design point. NPSHR is calculated by Cornell Pump in our test lab empirically. It is important to remember that the NPSHR will vary at different operating conditions for a pump, and can be different for the same operating conditions when comparing two different pumps.
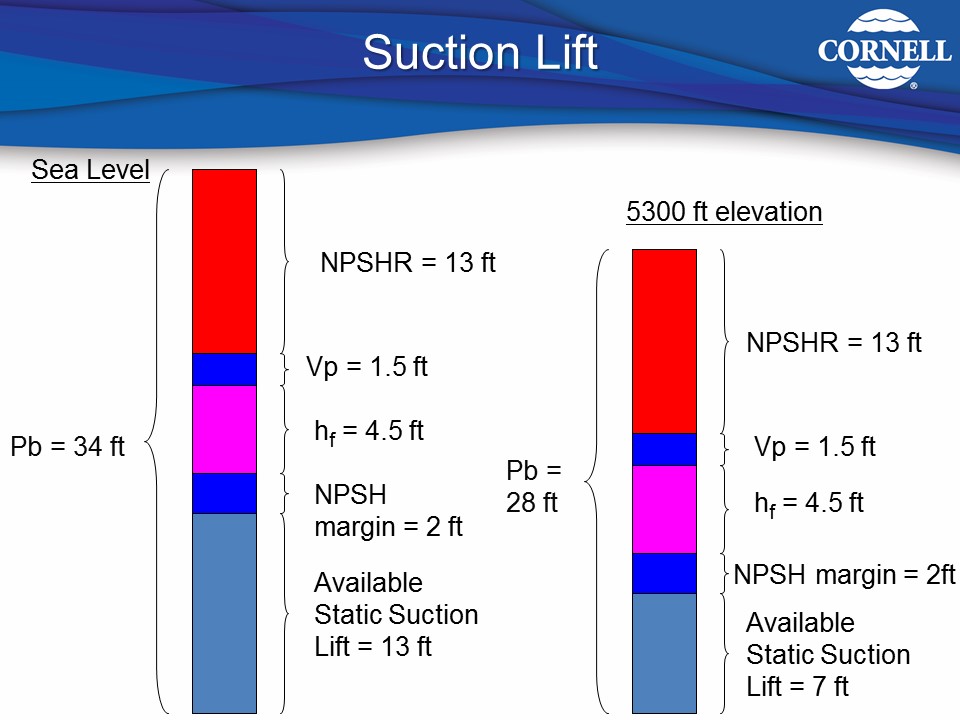
Next, the maximum a centrifugal pump can pull is constrained by nature. Atmospheric pressure exerts about 14.7 pounds per square inch of force on everything (you, a car, liquid) at sea level. That 14.7 psi on liquid allows it a maximum of 34 feet of head (push) at sea level. Again these values have been calculated for you. Not by pump manufacturers per se, but starting with enlightenment scientists looking to understand barometric and atmospheric pressure. Atmospheric pressure is understood today to be about 34 feet of head at sea level. If you were on the top of Mount Everest the psi would only be 4.4 and the energy impart would be 10.2 feet of head as a maximum.
So, you have a known amount in NPSHR provided by the pump manufacturer for the particular model, and you can consult a chart on atmospheric pressure.
In the third step, you have to do some leg work and round up everything (pipes, valves, etc.) that the liquid will travel through. Each of these items are not completely smooth, and in the case of elbows etc. are not straight either. Liquid moving through the parts will lose some energy running over the less than smooth bumps that exist (like a stream running into a rock—it gives up some energy and creates an eddy behind the rock.)
You will need to subtract all other losses from the equipment in order to determine the NPSHA of your system. Losses would also include your static suction lift in feet or the vertical distance from the water level to pump. The friction loss in feet in the suction pipe or the pressure lost when the water rubs against the walls of the pipe and losses created from vapor pressure which is a result of the temperature of the liquid.
It also advisable to include a safety factor to NPSHA. In case of storms (causing lower atmospheric pressure), changes in pipe diameter due to corrosion, etc., the factor allows the pump to operate in less than ideal conditions. Cornell recommends adding 2’ of loss for the NPSH margin.
Finally, once you know the losses for your NPSHA, you can add that to NPSHR, and then compare it the atmospheric pressure for the elevation. That will be the amount of static lift available.
Note: In order to avoid cavitation and pull a suction lift with your pump the NPSHA of your system must always be higher than the NPSHR (of the Pump).
The equation for determining how much of a suction lift you can pull with your pump you can take your Atmospheric pressure(Pb) subtract your Pump NPSHR, Vapor Pressure (Vp), friction losses (hf) and NPSH Margin (Safety factor) and you will have your maximum suction lift.
- Suction Lift = P(b) – (Ls + Vp + hf + NPSHR)
- P = Pressure (in ft) at surface of water
- Pb = Barometric Pressure (open system)
- P = Absolute Pressure at surface of liquid (closed system)
- Ls & Lh = Distance from water level to pump CL
- Ls is below pump centerline
- Lh is above pump centerline
- hf = Friction Losses in Suction Pipe
- Vp = Vapor Pressure of liquid.
- NPSHR (from pump curve)